最高のコレクション 割り算 と 分数 232193-割り算 と 分数

分数も当然、割り算の形で表せるということになります。 このように 分数は上 (分子)÷下 (分母)で表すことができます。 この考え方から 分母と分子が分数になったとしても このように計算できるというわけです。 この計算に慣れてきた人は、この 分数の割り算を掛け算にするときには、わる数の逆数（分数の分子と分母を入れかえる）をかけます。 ⇒ 分数の割り算やり方と問題 計算のとちゅうで約分できるので、約分をしてから計算をします。 × ÷ ＝ × × ＝ 答え 問題③ － × ÷2 はじめに、帯分数 を仮分数 に直します。 足し算・引き算よりも掛け算・割り算を先に計算するという四則演算のルール（計算の順序）があるので 数学・算数 割り算は分数に置き換えれることができますが なぜ、「割られるかず÷割るかず」が、 等分した大きさの つ (例：2分の1、3分の1とか)に 当てはめれるのか、わかりません。

分数とは割り算の答えである 妹z会中学受験コース4年

割り算 と 分数

割り算 と 分数- と分数のわり算の答えがわかってしまいます。 タエ子のテスト用紙に見える問題を「分母をそろえる」方法で解くことができます。 1/3÷3/10＝10/30÷9/30＝10÷9＝10/9 1/3÷3/5＝5/15÷9/15＝5÷9＝5/9 2/5÷3/7＝14/35÷15/35＝14÷15＝14/15 「分数のわり算はひっくり返してかけ算にする」という計算手順を覚えるのではなく、きちんと2/3の中に1/4がいくつあるか分数はひっくりかえしてかける と覚えるといいですよ。 練習問題 帯分数÷分数、整数÷分数、分数÷整数のしかたを考えさせ、練習問題に取り組ませます。 ※帯分数－仮分数の直し方のおさらい 続きはこちら(分数の割り算文章題) イラスト提供元

分数から割り算にする方法 迷ったらこのように覚えると楽 中学や高校の数学の計算問題

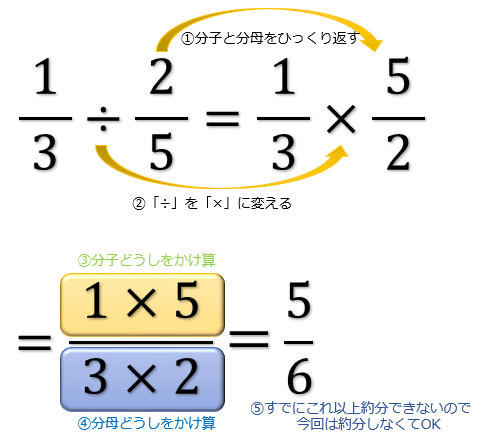
 第 6 回のテーマは「 分数の概念と計算方法 」です。 割り算 , 割合 , 比の「 変形 」である「 分数 」についての話です。 今までの「 割り算 , 割合 , 比 」の知識 は、この「 分数 」を理解することで 全てが繋がり、完成します 。 分数は小数とも密接な関わりがあります。 分数の割り算はひっくり返す！ 分数の割り算は、たった一つの動作で掛け算に変身します。 割る数の分子と分母を逆にする これだけです！ そうすれば、÷を×に変えることができます。 この分子と分母を逆にしたものを、「逆数」と呼んだりします。分数の割り算の解説 分数の割り算は、割るほうの分数の分子と分母を逆にして掛け算をおこなうことでできます。 約分が可能であれば約分までおこないましょう。 約分の電卓 1 2 ÷ 3 4 割り算（逆数の掛け算） = 1×4 2×3 = 4 6 = 2 3 分数の分子と分母を反対にしたものを 逆数 (ぎゃくすう)と言います。 AをBで割ることは、AにBの逆数を掛けるのと同じという法則があります。 この法則を利用して分

 分数のわり算を扱うときには「包含除」で考えることが理解するうえでの近道となります。 分数のわり算は、以下のように計算しますね。 4 ÷ 2 5 =4 × 5 2 = 10 4 ÷ 2 5 = 4 × 5 2 = 10 この式だけで説明しようとすると理解しにくいと思いますので、まずは簡単な例で考えてみましょう。 関連記事 二次方程式が「図形」で解ける!? また、分数と割り算は見た目（表し方）がちがうだけで、正体は同じです。 分子は割られる数で、分母は割る数 と同じ意味なのです。 ↓ これを割り算に直すと、 定義 割られる数÷割る数 になります。 分数の上の段を割り算記号の左に、分数の下の段を割り算記号の右にもってくる と覚えてOKです。 さて、直し方がわかったところで、1つの例題を見ていきます。 1/5を割り算に直すと ・割り算を分数で表そう。 ①のやり方は分子と分母をひっくり返して掛け算をする方法でした。 一方②のやり方は、÷3なら「3を分母にするだけ」という方法です。 ÷5なら分母を5にするだけです。 これを覚えておけば簡単に分数にできます。 ①や②のどちらのやり方でもできますが、⑤の問題のように分数にしてから、約分ができる場合もあるので、注意してください。 次の記事

 割り算は、 定義 割られる数÷割る数 というものです。 また、分数は上の段と下の段に分かれていますよね。 上の段を「分子（ぶんし）」といい、下の段を「分母（ぶんぼ）」 といいます。 分子は割られる数で、分母は割る数 と同じ意味なのです。 ↓ つまり、割り算と分数の関係をイラストであらわすと、次のようになります。 割り算記号の左を分数の上の段に、割り算記号の右を分 分数の割り算の理解その2（繁分数の利用） であることなどを使うと すなわち です。 これは上の「÷」の起源を考えれば、ごく直感的な表し方になっています。 分数÷分数にもこれを応用すると です。 このような を繁 (はん)分数といいます。 そして、この繁分数の 分母が になるように変形 していきます。 繁分数が気持ち悪くなければ、分数の割り算はこのように考えることもできます割り算は分数で表せる ・・・\(2\div 3=\dfrac {2}{3}\) 分母と分子に同じ数をかけても分数の値は変わらない ・・・\(\dfrac {2}{3}=\dfrac {2\times 2}{3\times 2}=\dfrac {4}{6}=\dfrac {2}{3}\)

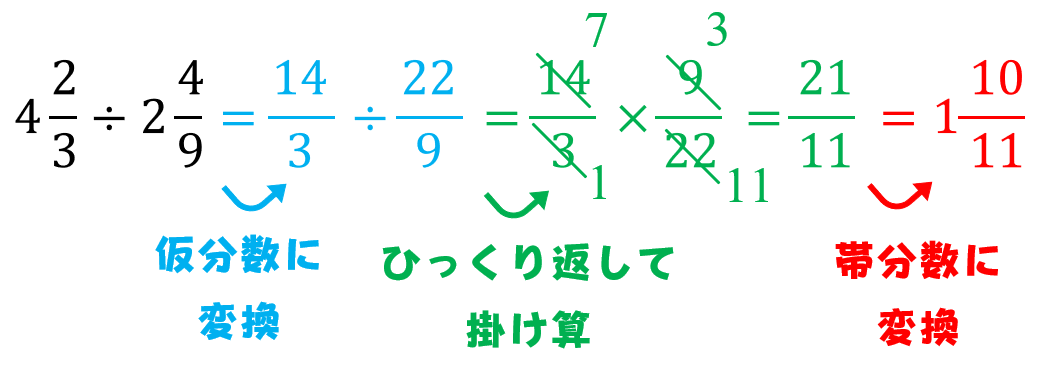
帯分数の計算方法 足し算 引き算 掛け算 割り算 小学生への教え方のポイント 数学fun

小6算数 分数のわり算 指導アイデア 2 みんなの教育技術

 割り算の商と分数は、下の式の関係になることに注意して問題を解きましょう。 $$\Large{a}\div{b}=\frac{a}{b}$$ ぴよ校長 さっそく問題を解いてみよう！ 「割り算の商と分数」問題集はこちら 下の問題画像や、リンク文字をクリックすると問題と答えがセットになったPDFファイルが開きます そのような割合のケースは、割り算を分数に置き換えたものとは等しくありません。 8÷2 は8/2と表現できますが、答えは一緒でも16/4とは違うものです。 ホールケーキを6等分した1個1個は、ホールケーキまたは全体の6分の1です。 その内の2個は、ホールケーキまたは全体の6分の2つまり3分の1です。 （分数表示されていますが、割り算ではありません） あくまでも全体の6分の1 分配法則とは？ 証明や分数・割り算を含む計算問題 21年11月5日 この記事では、分配法則の成り立ち（証明）や、分配法則を利用する計算問題の解き方などを解説していきます。 小学生のときに習ったことを思い出しながら読み進めてくださいね

3

すきるまドリル 小学６年生 算数 分数のわり算 無料学習プリント すきるまドリル 幼児 小学生の無料学習プリント

 割り算「/」 これは、もともとタイプライターの時代に、分数を上下に打つことができなかったので、使われました。 パソコンになっても、 「÷」の記号はないので「/」を使います。 分数の「ー (横棒) 」を「ななめ」にしたと思ってください。 割り算とは、 割られる数 である「 全体量 」と、 割る数 である「 単位量あたりの大きさ 」と「 いくつ分 」の 3 つの関係 で成り立っています。 割り算の意味と仕組み 割り算には 3 つの意味 があります。 分ける ( 等分除 )、一番適用範囲の広い「 あらゆる意味で分ける 」 いくつ含まれるか ( 包含除 )、大きい数を小さい数で割る 比べる ( 割合や比を表す ) これらは、場面や状況で意味が決無料ダウンロード・印刷できる小学5年生の算数わり算と分数の練習プリントです。 分数にある2つの意味のうち、第一義 （ 1を3等分したものを2つ集めたもの＝ 2/3 ）は3年生で学習します。 このページのプリントでは、 第二義 （ 2を3でわったもの＝ 2/3 ）つまり、わり算の商を表すための分数 (商の分数） を中心に、その表し方や計算方法を練習します。 わり算と分数（商分数）（1） 答え

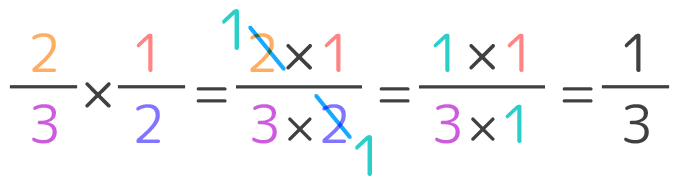
小6 分数と分数の割り算 のやり方は 逆数のかけ算になる理由 そうちゃ式 分かりやすい図解算数 別館

分数 整数 の割り算 計算ドリル 問題集 数学fun

3年生算数ドリル ～分数～ 練習問題プリント Tweet もくじ 1九九の表とかけ算 11百マス計算 1のかけ算 13 にあてはまる数 2わり算 21分け方とわり算 22あまりのあるわり算 33けたのひっ算 31何百のたし算とひき算 323けたのたし算のひっ算 333けたのひき算のひっ算 44けたの割り算 分数の割り算は、割る数を逆数にして掛けること で計算できます。 文字式で表すと次のようになります。 分数の割り算のやり方 a b ÷ c d = a b × d c a b ÷ c d = a b × d c このページでは、 分数の割り算のやり方 と 計算のコツ を例題と共に説明しています。 そして 割る数を逆数にして掛ける理由 も説明しています。 もくじ 分数の割り算のやり方基本 分数 分数とは 分数とは、「1つの物を、何個に切ったうちの何個分」と表すことができる数字です。はじめのうちは、分数が出てくるたびに「何個に切ったうちの何個分」と頭の中で考えて、だいたいどれくらいの大きさの数なのか想像するようにしましょう。

分数の割り算の計算プリント 帯分数編 全180問無料 算数パラダイス

分数のわり算２ 分母どうし分子どうし割ってはいけないか

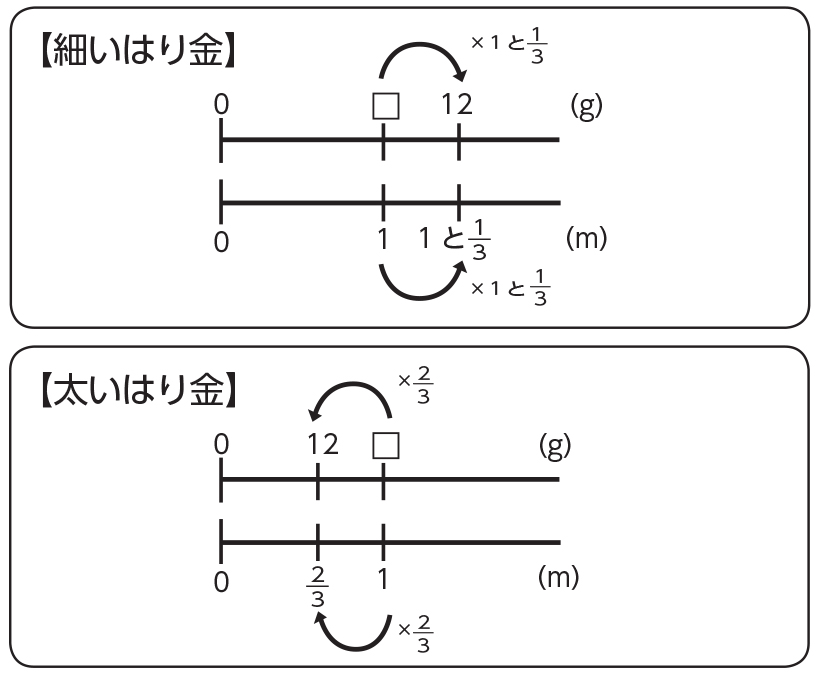
小学5年生の算数 わり算と分数｜商分数／分数の第二義 練習問題プリント 分数にある2つの意味のうち、第一義 （ 1を3等分したものを2つ集めたもの＝ 2/3 ）は3年生で学習します。 このページのプリントでは、第二義 （ 2を3でわったもの＝ 2/3 ）つまり、わり算の商を表すための分数 (商の分数）を中心に、その表し方や計算方法を練習します。 （プリント10枚）④ 分数倍の意味と分数倍を使った割合の考え方、分数の積の大きさ 教え方1 はじめに5年生の小数×整数のおさらいをさせましょう。 問題①5年のおさらいの問題 1dLで0．6 ぬれるペンキがあります。 3dLでは、何 ぬることができますか。 1dLでぬれる面積 × ペンキの量 と考えると 式は 06＝18 すると となります。 次に1つ目の式をx=～の形にします。その際、 両辺をy 3/2 で割ります。それはつまり両辺をy ー3/2 でかける ということになります。ここでこの割り算や分数は－1乗するというポイントを使いました。

分数の割り算のやり方 大人のやり直し算数の第一歩 計算方法の解説 無料

数学塾直伝 分数の割り算の教え方と詳しい理屈 どうしてひっくり返すのかがよくわかる 永野裕之のblog

帯分数 帯分数 の割り算 計算ドリル 問題集 数学fun

分数のかけ算わり算 まとめ 小学生 算数のノート Clearnote

小学６年生の算数 分数のわり算 分数 整数と分数 分数 練習問題プリント ちびむすドリル 小学生

平方根の割り算は 1分でわかる計算 割り算の問題とやり方 有理化 分数との関係

小学生向け 算数 プリント 分数同士の割り算 学習塾 Step By Step

分数の割り算はなぜひっくり返してかけるのか その理由を説明する3つの教え方 逆数をかける理由 アタリマエ

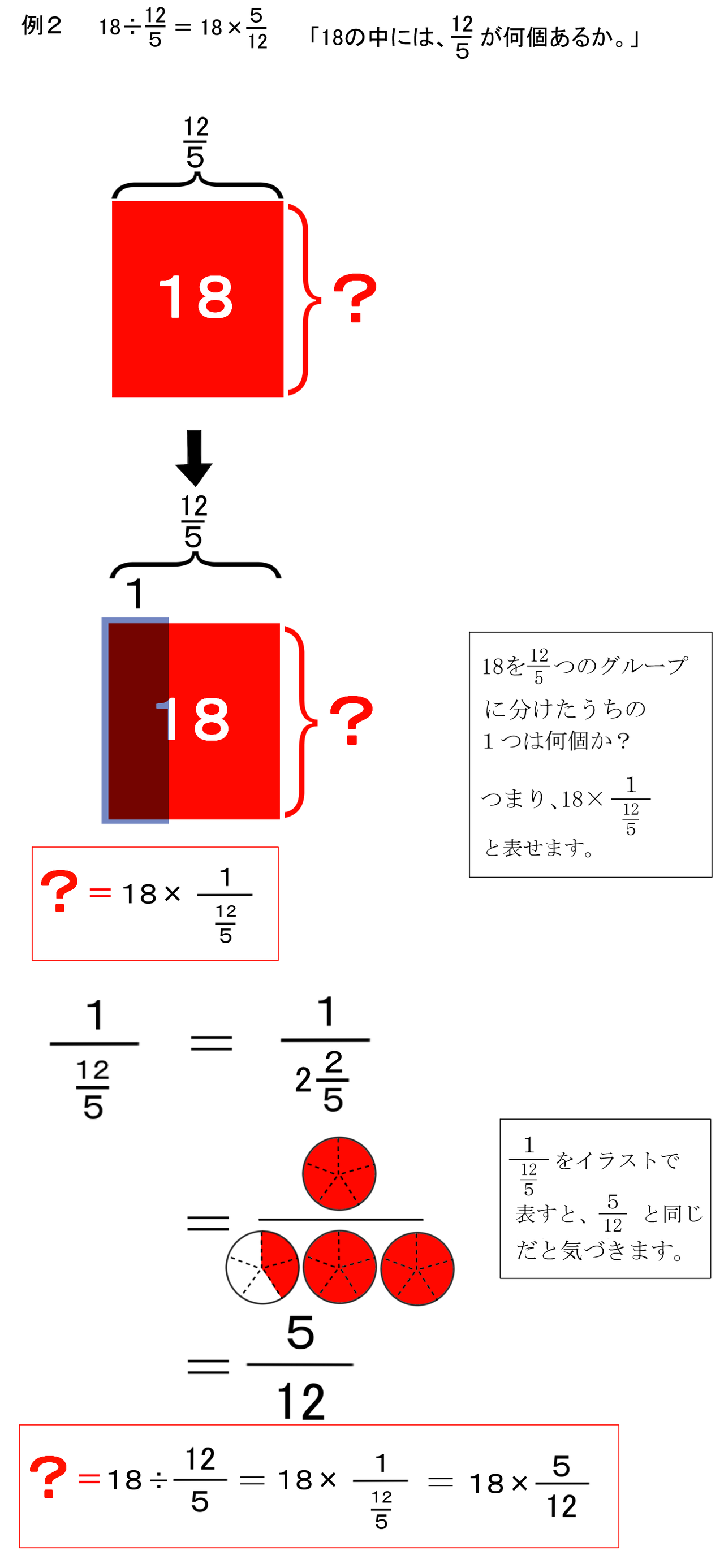
疑問１ なぜ分数の割り算では 分子と分母を逆にするの バカでもわかる 中学数学

分数の割り算はなぜひっくり返してかけるのか その理由を説明する3つの教え方 逆数をかける理由 アタリマエ 分数 割り算 小学校 算数

1

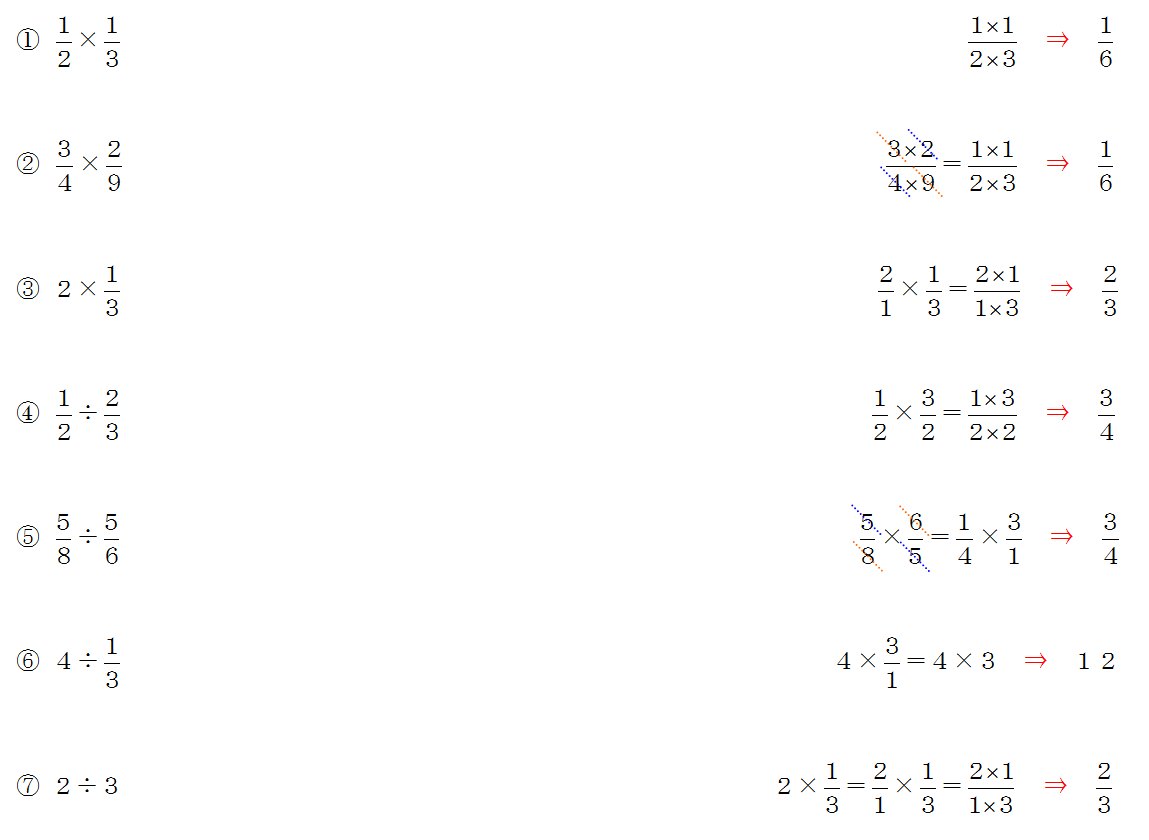
分数の掛け算と割り算の問題 やり方は非常に簡単 約分にだけ注意 三重の個人契約家庭教師

いえがくサポート 小６算数 分数の倍とかけ算 わり算

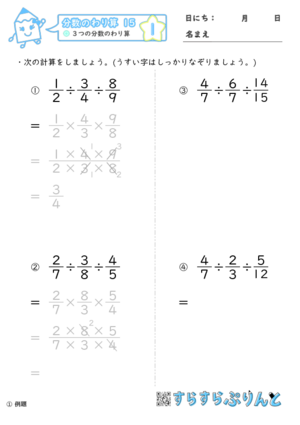
分数のわり算 ３つの分数のわり算 小学6年算数 無料プリント

コンプリート 分数 掛け算 割り算 シモネタ

割り算をしたとき その数は分母と分子のどっちに行くか覚えよう 中学や高校の数学の計算問題

分数の割り算の考え方と解き方 なぜ割る数を逆数にしてかけるか Cocoiro ココイロ Part 3

分数の割り算をどう学ぶか 解答募集 Raising Kids With English Is So Much Fun 楽天ブログ

分数の割り算の問題 やり方は逆数をとってかけるだけ 中学や高校の数学の計算問題

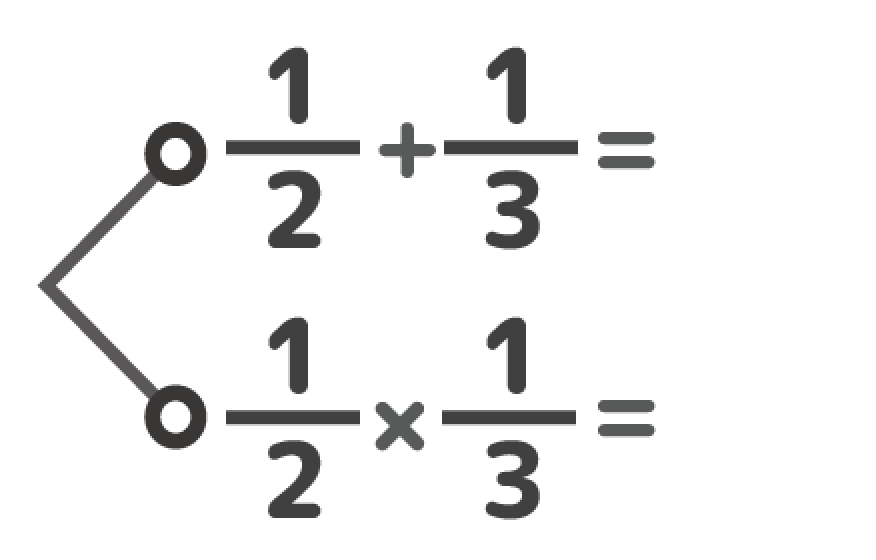
小6への分数の教え方のコツ 計算方法の違いを理解させる かけ算割り算と 算 算 そうちゃ式 分かりやすい図解算数 別館

分数の計算プリント全12種 約3000問無料 解説 回答つき 算数パラダイス

小学６年生の算数 分数のわり算 分数 整数と分数 分数 練習問題プリント ちびむすドリル 小学生

小学６年生の算数 分数のわり算 分数 整数と分数 分数 練習問題プリント ちびむすドリル 小学生

小学６年生の算数 分数 整数のわり算 練習問題プリント ちびむすドリル 小学生

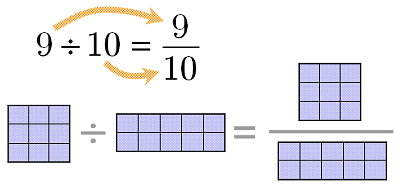
初等代数 分数を教える 割り算 大人が学び直す数学

分数の割り算のやり方 大人のやり直し算数の第一歩 計算方法の解説 無料

小学6年生 算数 無料問題集 分数 分数の約分のある割り算 おかわりドリル

正負の数の四則計算 中学数学計算の優先順位と理由 リョースケ大学

多項式の掛け算 割り算と分配法則 代入計算のやり方 リョースケ大学

分数割り算 ６年生 算数問題 計算プリント

分数の割り算はなぜ逆数をかけるのか 小学生の子供に説明する方法 数学fun

平方根の計算 ルート分数の割り算の仕方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

なぜ分数の割り算はひっくり返してかける 分数の定義と逆数について 趣味の大学数学

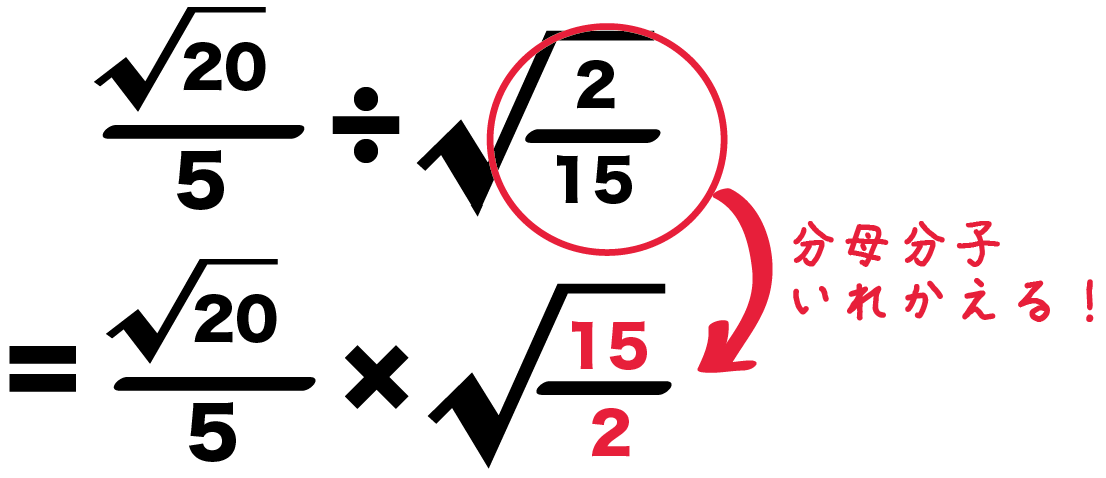
平方根の計算 ルート分数の割り算の仕方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

新版 なぜ分数の割り算はひっくり返すのか By 板橋 悟

わり算２ オイラーに習う分数の割り算 大学への算数 Ena国際部

238 0はどっちからどっちを割るのですか 分数では分母を分 Yahoo 知恵袋

分数の割り算のやり方 大人のやり直し算数の第一歩 計算方法の解説 無料

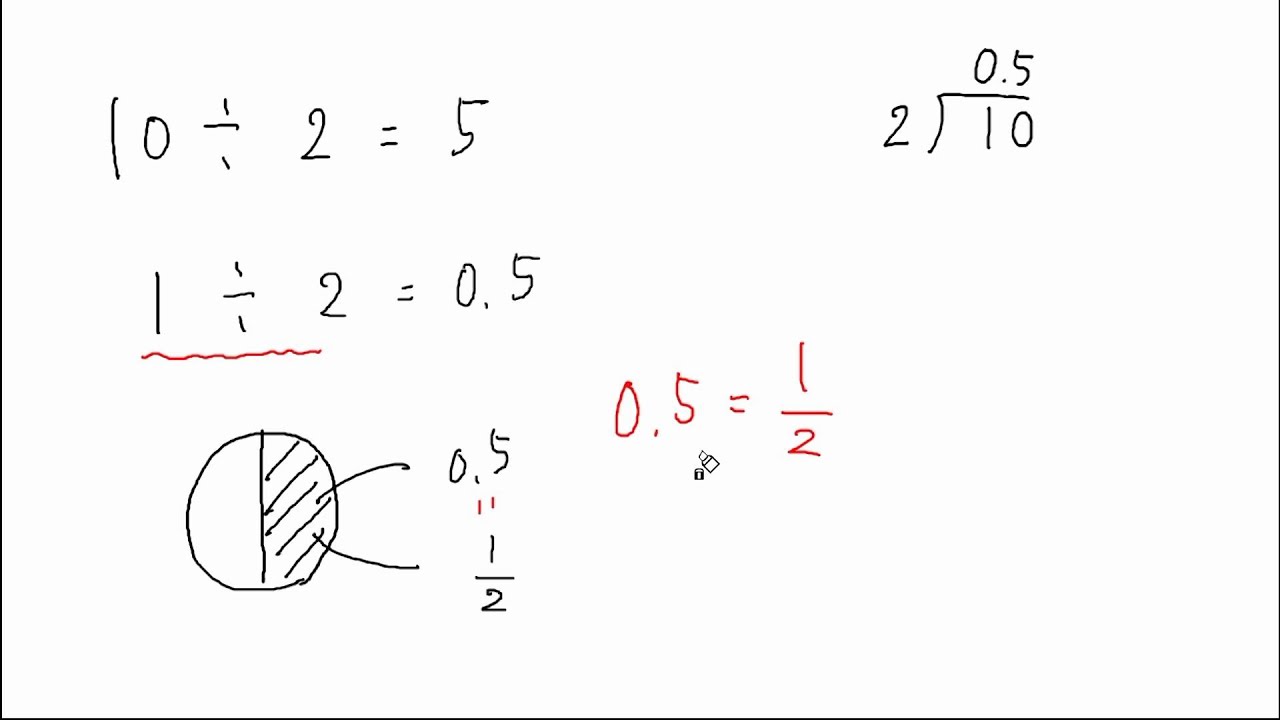
わり算 商 を分数で表す Youtube

分数の割り算の計算プリント 真分数編 全240問無料 算数パラダイス

分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ

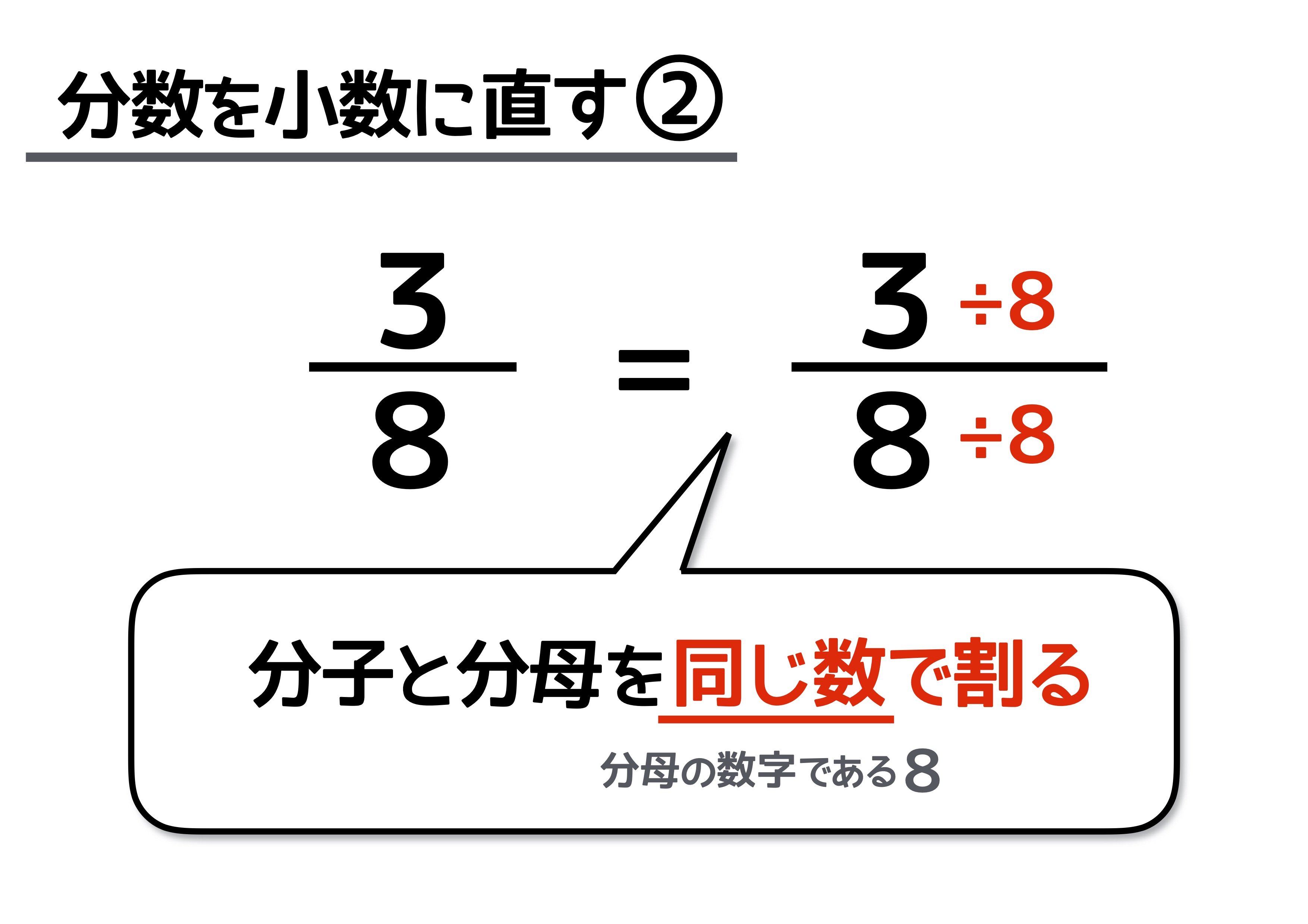
分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ

割り算は2種類あるって知っていますか ー算数嫌いの子のための算数 I Learn Jp

分数とは割り算の答えである 妹z会中学受験コース4年

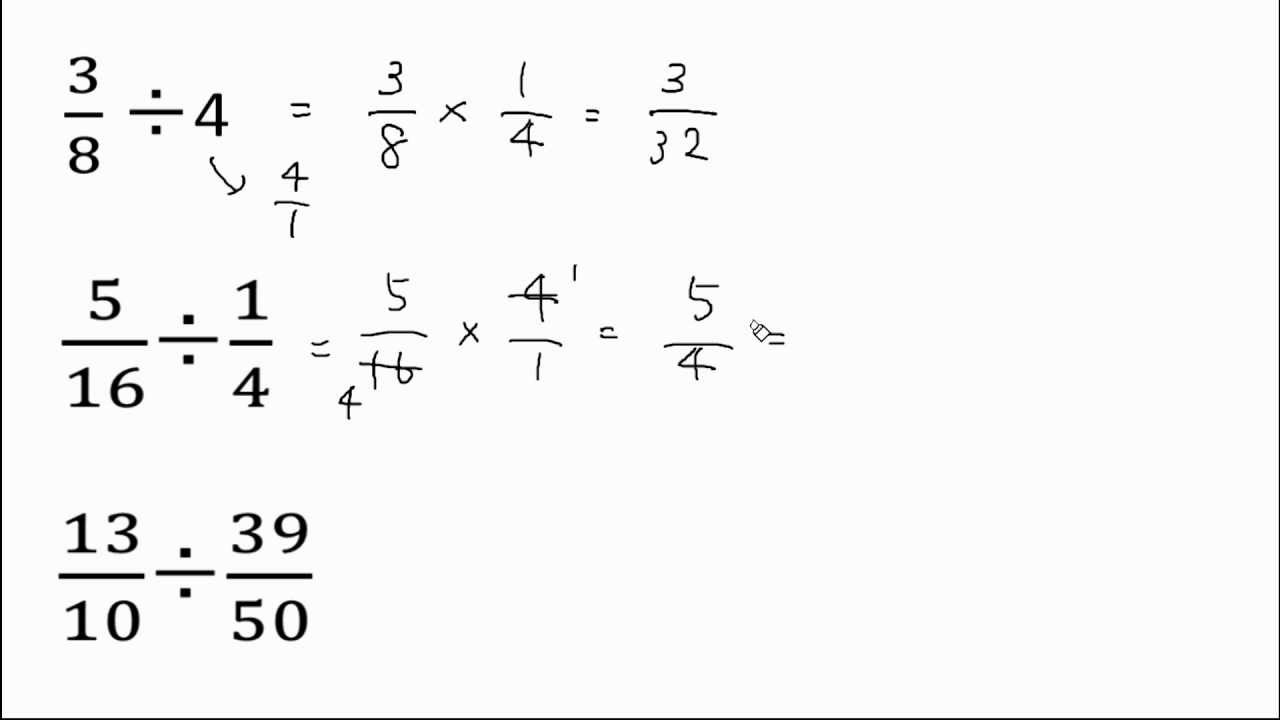
分数のわり算 問題練習 Youtube

分数を使いこなそう かけ算 わり算と分数 後編 桜花 現役バイト塾講師 Note

6年生算数ドリル 分数 分数のわり算

分数から割り算にする方法 迷ったらこのように覚えると楽 中学や高校の数学の計算問題

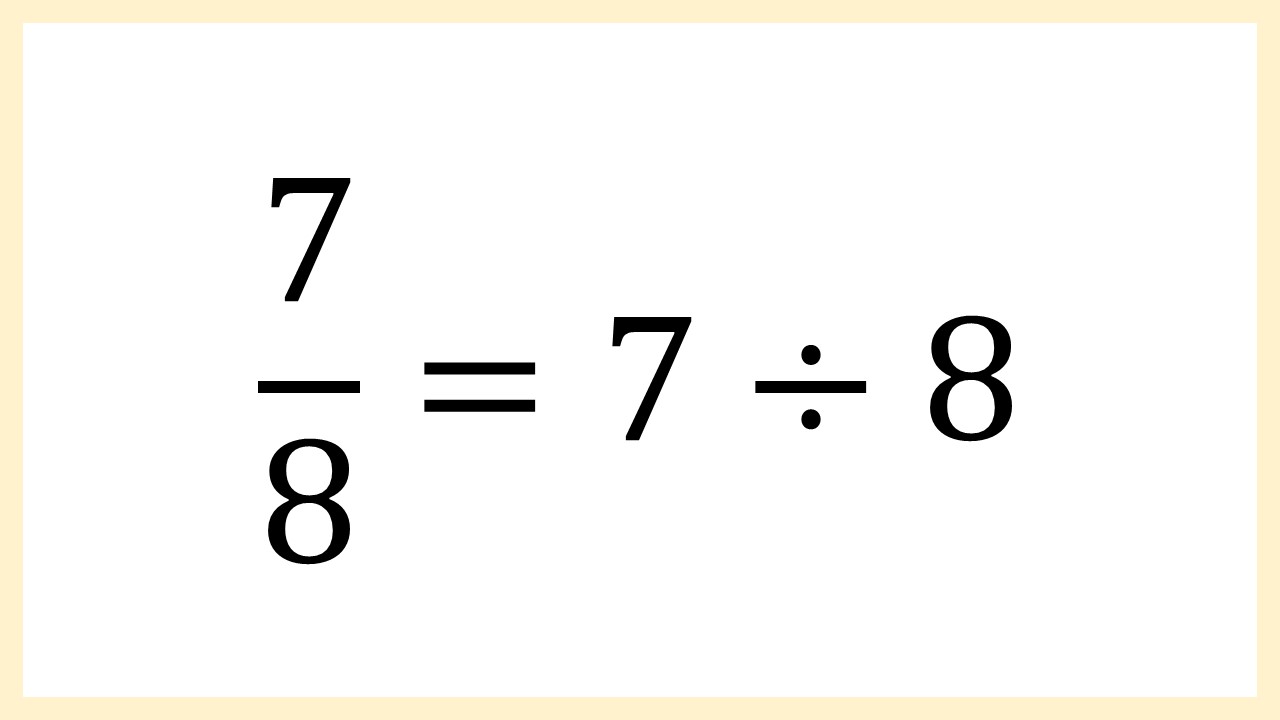
よくわかる 分数を割り算に直す方法 例題あり

分数の割り算 なぜひっくり返す 分母をそろえて 朝日新聞デジタル

分数の割り算 3 5 1 2 ビデオ 分数を分数で割る カーンアカデミー

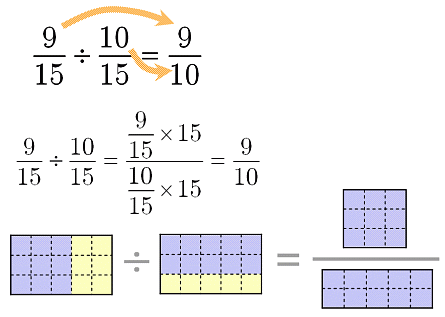
初等代数 分数を教える 割り算 大人が学び直す数学

文字を使った式のルール その１ Gains ゲインズ ネットスクールの資格取得応援情報サイト

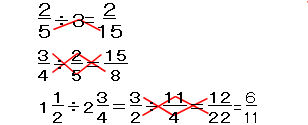
分数のわり算4

割り算を分数で表す問題 分数にするにはこれを覚えておけばｏｋ 中学や高校の数学の計算問題

小学６年生 算数問題プリント

初等代数 分数を教える 通分 約分 足し算 大人が学び直す数学

分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ

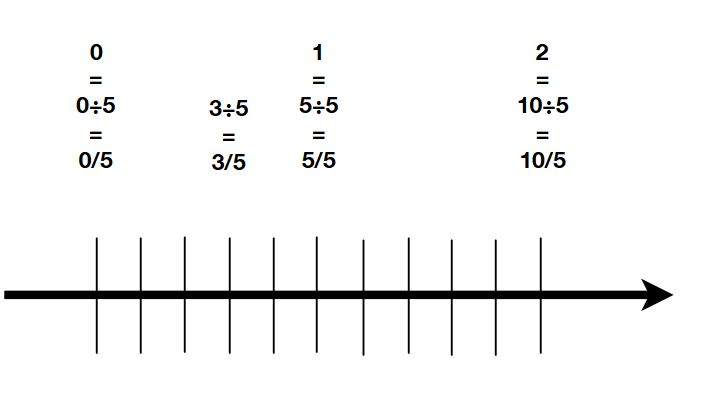
分数のわり算 等分除 包含除 を数直線で かけ算の順序の昔話

分数の割り算はなぜひっくり返してかけるのか その理由を解説 空間情報クラブ 株式会社インフォマティクス

わり算と分数 何倍と表せばいいのかな 国際算数数学授業研究プロジェクト Impuls International Math Teacher Professionalization Using Lesson Study

6年生算数ドリル 分数 分数のわり算

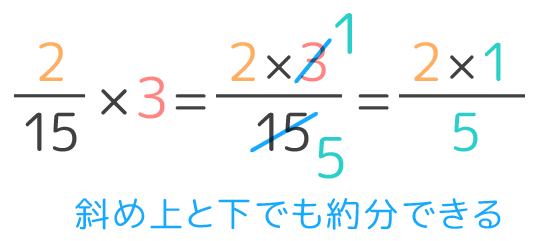
小学5年生 帯 真 分数と整数の割り算 を図解 そうちゃ式 分かりやすい図解算数 別館

分数を小数にするやり方 大人のやり直し算数の第一歩 計算方法の解説 無料

小学５年生の算数 わり算と分数 商分数 分数の第二義 練習問題プリント ちびむすドリル 小学生

分数のかけ算わり算 まとめ 小学生 算数のノート Clearnote

分数の割り算のやり方 大人のやり直し算数の第一歩 計算方法の解説 無料

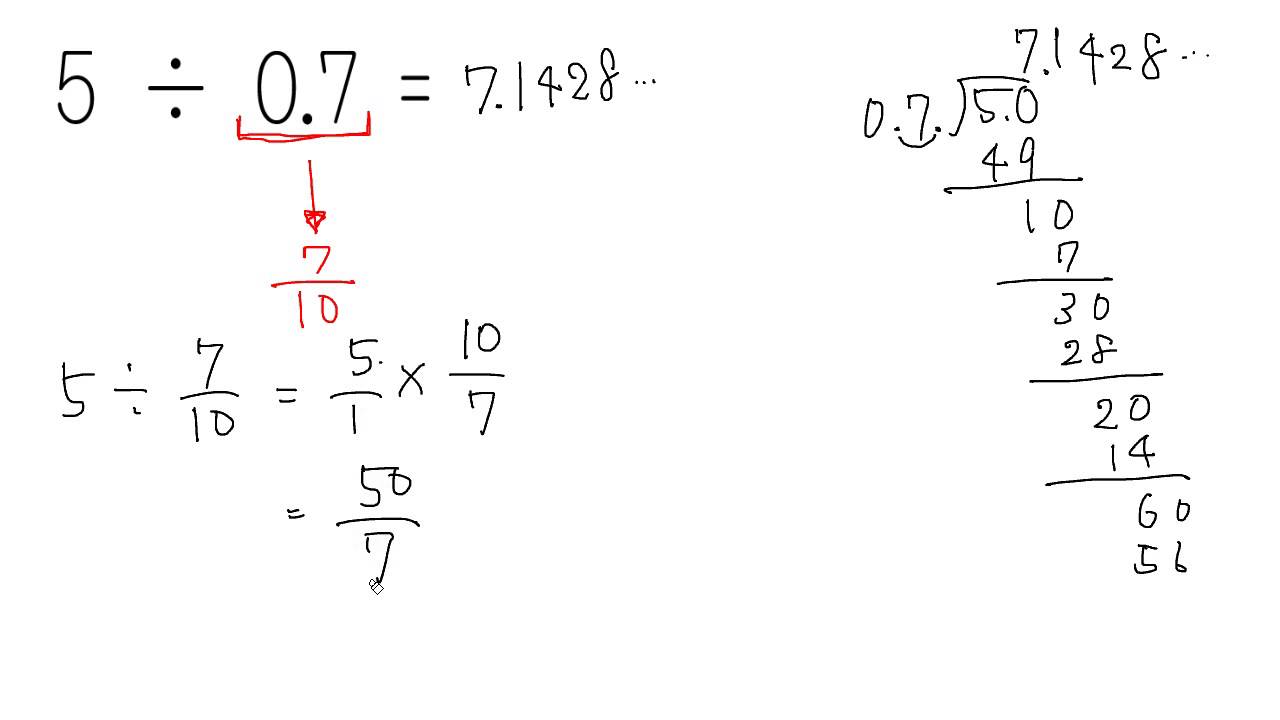
分数と小数の混じったかけ算 割り算 Youtube

分数の割り算 Youtube

何で分数の割り算は逆数をかけるの 理由を説明できますか

小学生向け 算数 プリント 分数同士のかけ算 割り算テスト 学習塾 Step By Step

整数の割り算を分数にする練習 5年生 分数と小数 整数 まなび365 無料算数プリント

分数計算 間違えが続出する帯分数の割り算 ネタファクト

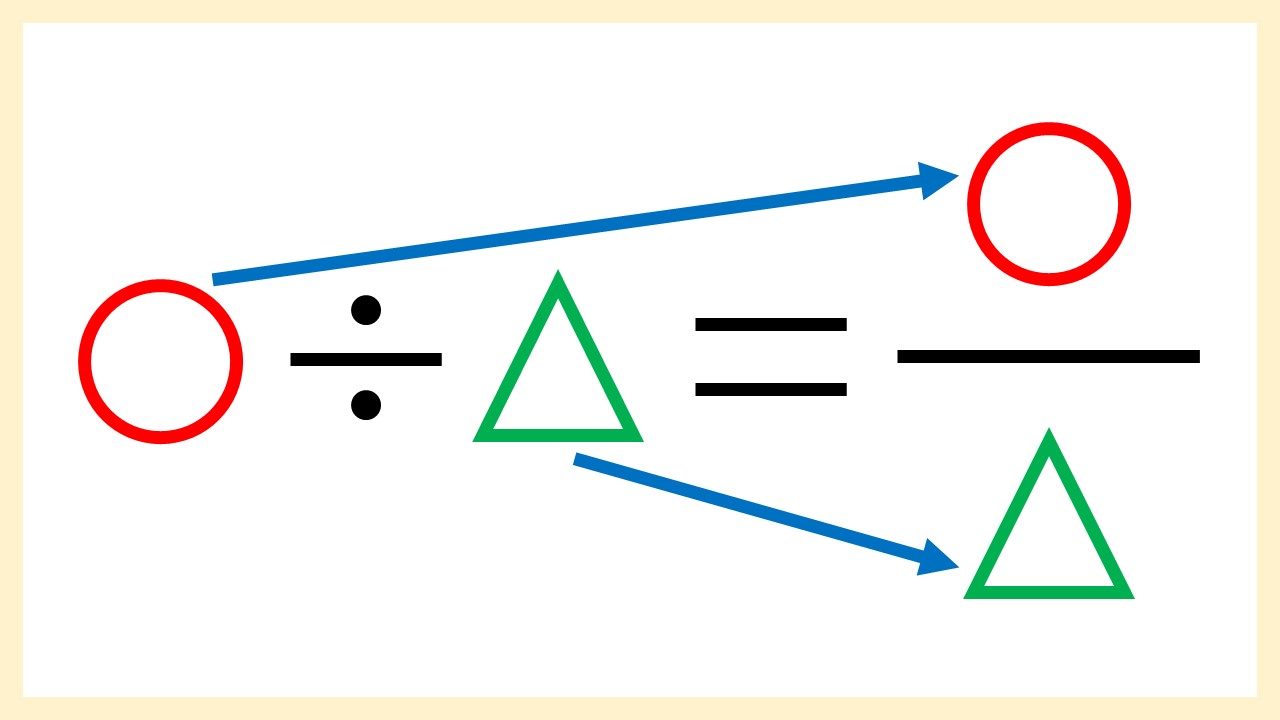
よくわかる 割り算を分数に直す方法 例題あり

小学６年生の算数 分数のわり算 分数 整数と分数 分数 練習問題プリント ちびむすドリル 小学生

小学6年生 算数 無料問題集 帯分数 帯分数の約分の無い割り算 おかわりドリル

1

小５ 算数 小５ ２７ わり算と分数 基本編 Youtube

帯分数の計算方法 足し算 引き算 掛け算 割り算 小学生への教え方のポイント 数学fun 小学校 算数 算数の教え方 数学

小学5年生 算数 無料問題集 割り算の商と分数 おかわりドリル

分数の割り算のやり方 大人のやり直し算数の第一歩 計算方法の解説 無料

小学6年生の算数 動画 分数のわり算 の問題 19ch

中1数学 正負の数 分数計算のやり方を問題解説 数スタ

小６ 算数 小６ ８ 分数のわり算 Youtube

1

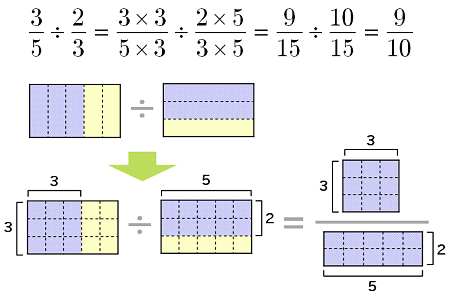
初等代数 分数を教える 割り算 大人が学び直す数学

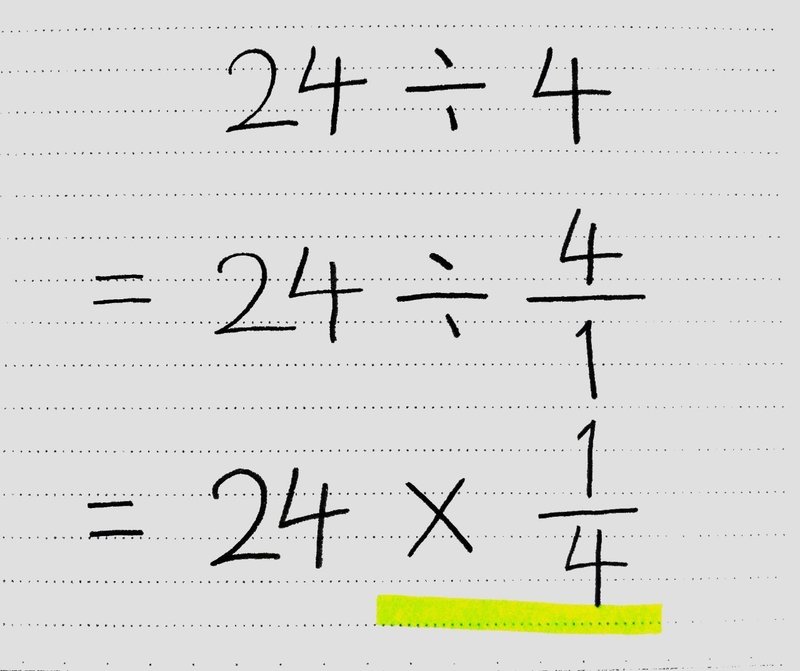
分数を使いこなそう かけ算 わり算と分数 後編 桜花 現役バイト塾講師 Note

わり算２ オイラーに習う分数の割り算 大学への算数 Ena国際部

分数の掛け算の上手な教え方 なぜ分母同士 分子同士をかけるのか 数学fun

分数の割り算のやり方 大人のやり直し算数の第一歩 計算方法の解説 無料

平方根の割り算は 1分でわかる計算 割り算の問題とやり方 有理化 分数との関係

驚きの割り算の意味 割り算って本当は比だった 確かに 単に分けるという考えでは分数になったとたん説明出来ないよね ハーフの子どもたちの日本語継承語教育と考える力を育む どんぐる教室 In ルクセンブルク

分数の割り算は割り算の分数 1ncrement

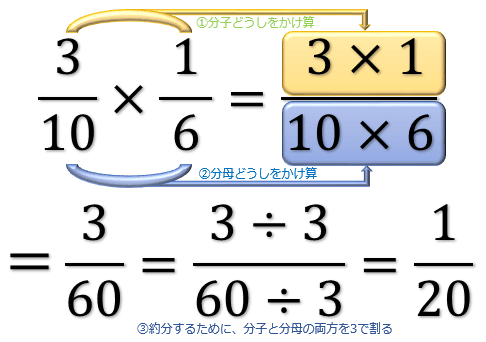
分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ

すコラ 08 12 03 わかりやすい分数の割り算 その2 号外 やまねこ新聞社

小学5年生向け分数のかけ算問題

Incoming Term: 割り算 と 分数,